SIR模型简介
SIR模型将总人口分为以下三类:易感者(susceptibles),其数量记为s(t),表示t 时刻未染病但有可能被该类疾病传染的人数;染病者(infectives),其数量记为i(t),表示t时刻已被感染成为病人而且具有传染力的人数;恢复者(recovered),其数量记为r(t),表示t时刻已从染病者中移出的人数。设总人口为N(t),则有N(t)=s(t)+i(t)+r(t)。
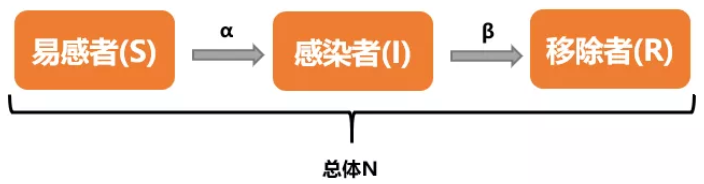
SIR模型的建立基于以下三个假设:
⑴不考虑人口的出生、死亡、流动等种群动力因素。人口始终保持一个常数,即N(t)≡K。
⑵一个病人一旦与易感者接触就必然具有一定的传染力。假设 t 时刻单位时间内,一个病人能传染的易感者数目与此环境内易感者总数s(t)成正比,比例系数为β,从而在t时刻单位时间内被所有病人传染的人数为βs(t)i(t)。
⑶ t 时刻,单位时间内从染病者中移出的人数与病人数量成正比,比例系数为γ,单位时间内移出者的数量为γi(t)。
基于以上三个假设条件,感染机制如下所示:
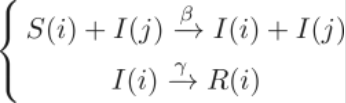
在以上三个基本假设条件下,可知:当易感个体和感染个体充分混合时,感染个体的增长率为βi(t)s(t)-γi(t),易感个体的下降率为βi(t)s(t),恢复个体的增长率为γi(t)。易感者从患病到移出的过程可以用微分方程表示如下:
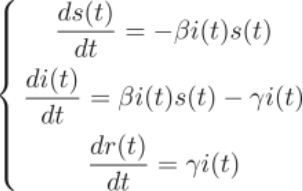
解得微分方程的解为
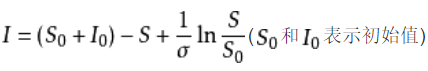
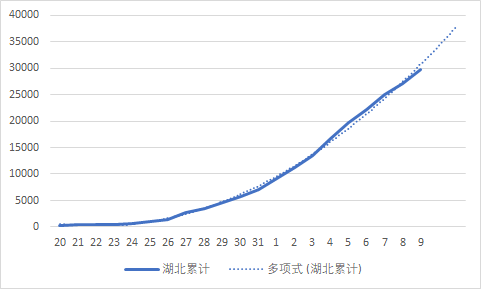
下图表示了随着时间t的变化S、I、R人数的一个变化趋势。
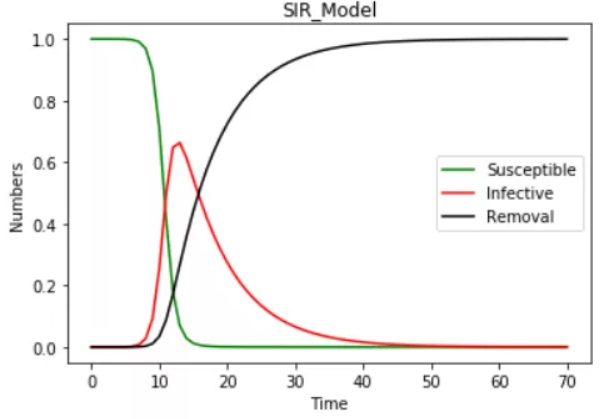
新冠肺炎分析
数据统计
下表为20日到9日的疫情数据(数据均来自湖北省卫生健康委员会)
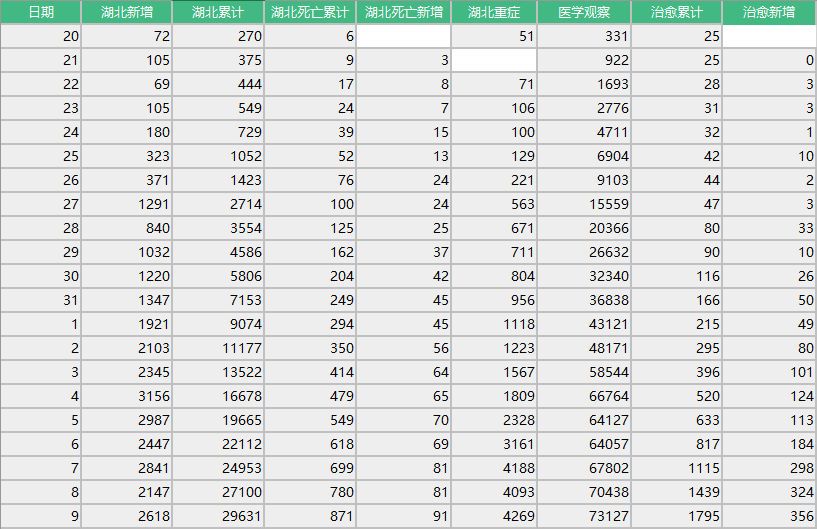
模型设定
0. 图像R^2 > 0.99则认为拟合良好,ΔR^2 < 0.01 则认为极其相似
1 月22~23日武汉与湖北13市相继封城,可认为人口常数稳定不变
经下图可知,从20日到5日湖北新增病例与医学观察的三次多项式拟合曲线几乎一致,可认为新增病例与医学观察人数线性相关,为正比关系
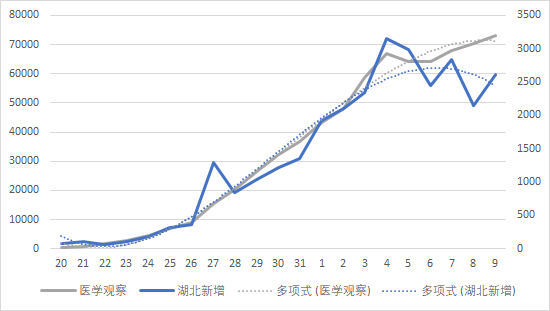
经下图可知,湖北死亡人数与重症人数多项式拟合曲线几乎一致,可认为重症病人的死亡率现阶段维持在一个比较稳定的数值
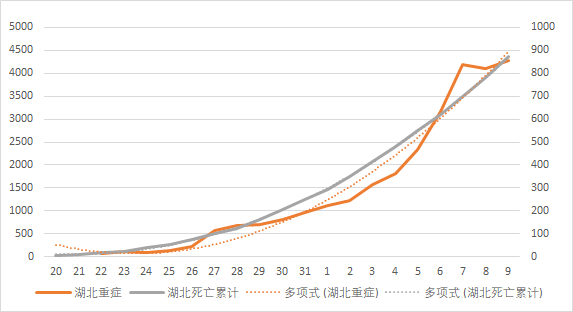
由下图知,近期湖北患者在以双曲线形式缓慢增长
定义与符号说明
s(t)——易感者——医学观察总人数
i(t)——感染者——湖北病例总人数
r(t)——恢复者——治愈累计总人数
d(t)——死亡人数
c(t)——重症患者人数
模型建立
感染机制:
*i(t)=γ s(t)/dt *
重症致死率:
d(t)=σ c(t)
模型求解:
- 重症患者在二月6日之前为指数增长,方程为
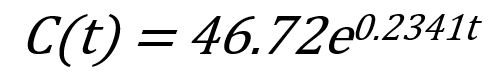
- 死亡人数
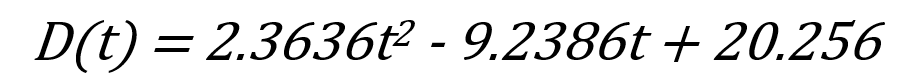
- 治愈人数
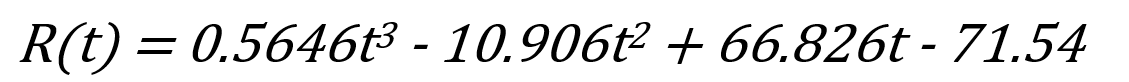
- 感染者人数
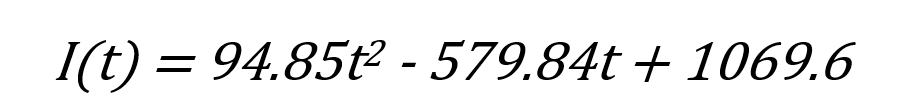
其他分析
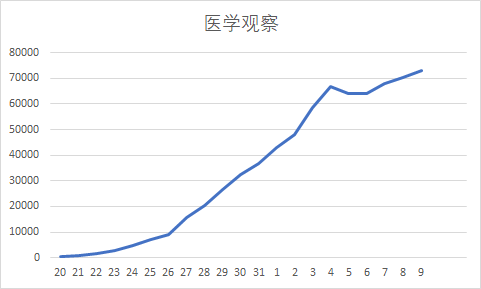
- 由下图可知,在二月3日之前医学观察人数可认为是一次函数增长,在3日突然被截止,可认为火神山开始接诊的功劳
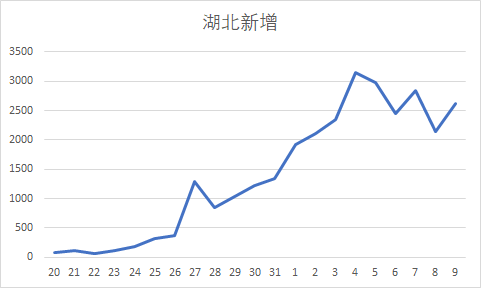
- 由下图可知,新增患者人数有几个突发期,对应几个关键点的作用,封城,诊断试剂的大批量制备,中央调查组的到来,加大了诊断力度
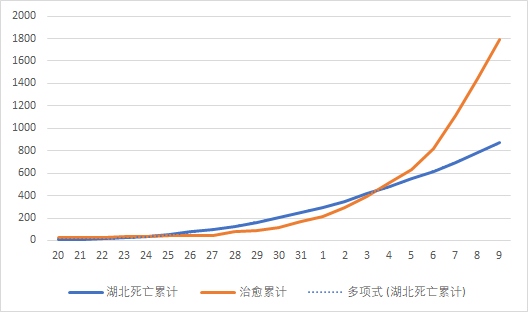
- 右下图可知,在4日之后,以治愈的人数超过死亡人数,ecmo的到来、瑞德西韦的专利申请和三期临床开始显效,当然也有莲花清瘟和双黄连的功劳
重大时间
- 一月3日,武汉已发现不明原因病毒性肺炎 44 例
- 一月23日,武汉市全城封城,公交地铁机场火车站等通道暂时关闭
- 一月24日,湖北省启动突发公共卫生事件一级应急响应
- 二月2日,火神山正式交付
- 二月3日,火神山开始接诊
- 二月6日,武汉开展全民测体温工作,每天逐户逐人全面排查
